Understanding the Formulation of Information Entropy
NOTE: The terms "language" and "word" are used metaphorically in this document.
A "language" often has many "words", and the frequency of each "word" varies.
If a "language" \(X\) has a total of \(n\) "words", then we can encode a word with \(\log_{2}{n}\) binary bits. But when transmitting the words, we want to keep the encoding of each "word" as short as possible. A common practice is that for those high-frequency "words", we can use shorter encodings, and for those "words" that we use less frequently, we can allow longer encodings. An example is the Morse code encoding for a "language" consisting of 36 "words" - 26 Latin letters and 10 Arabic numerals.

So, under some optimal encoding, what limit can the weighted average encoding length of all "words" achieve?
Suppose our "language" has \(n\) "words", \(x_1, x_2, \dots, x_n\), and their probability of occurrence is \(p(x_1), p(x_2), \dots, p(x_n)\) (known quantities).
Assuming that the lengths of the encodings of these "words" are \(L(x_1), L(x_2), \dots, L(x_n)\) respectively, the weighted average encoding length of each "word" is:
\(\bar{L} = p(x_1) L(x_1) + \dots + p(x_n) L(x_n)\)
How do we find the minimum value of \(\bar{L}\)?
Constraints
Obviously, the encoded length of all "words" is greater than 0. But beyond that, there is a hidden constraint.
We do not allow one encoding to be a prefix of another encoding, otherwise there will be ambiguity during decoding. For example, assuming that the three "words" of "A", "B", and "C" in the alphabet are encoded as "0", "1", and "01" respectively, then for For a code like "001", should we decode it as "AAB" or "AC"?
We call a type of code which requires that there is no whole code word in the system that is a prefix of any other code word in the system as a prefix code.
This means that if we assign a shorter encoding to a "word", it will squeeze a lot of resources out of the encoding space. For example, suppose the "word" "A" is encoded as "0", then it would "squeeze out" "00", "01", etc. from the codewords.
Suppose the maximum value in \(L(x_1), L(x_2), \dots, L(x_n)\) is \(L_{max}\). Then the encoding of all "words" are nodes on a full binary tree with a height of \(L_{max}\), and the full binary subtrees below each node have no intersection (otherwise violating the properties of the prefix code), as shown below.

It is obvious that, all the full binary subtrees below each node, at most cover all the leaves of the full binary tree with height \(L_{max}\).
For a "word" \(x_i, i \in \{1, 2, \dots, n\}\), the height of the full binary subtree below it is \(L_{max} - L(x_i)\), and it covers \(2^{L_{max} - L(x_i)}\) leaves.
As the full binary tree with height \(L_{max}\) has a total of \(2^{L_{max}}\), we have:
\(2^{L_{max} - L(x_1)} + 2^{L_{max} - L(x_2)} + \dots + 2^{L_{max} - L(x_n)} \le 2^{L_{max}}\)
This simplifies to:
\(2^{- L(x_1)} + 2^{- L(x_2)} + \dots + 2^{- L(x_n)} \le 1\)
This is the Kraft-McMillan inequality.
Optimization
Therefore, our overall optimization objective is:
\(\bar{L} = p(x_1) L(x_1) + \dots + p(x_n) L(x_n)\)
Subject to:
- \(p(x_i) \in (0, 1), i \in \{1, 2, \dots, n\}\) are constants
- \(p(x_1) + p(x_2) + \dots + p(x_n) = 1\)
- \(L(x_i) > 0, i \in \{1, 2, \dots, n\}\) are independent variables
- \(2^{- L(x_1)} + 2^{- L(x_2)} + \dots + 2^{- L(x_n)} \le 1\)
We can analyze the problem for the case where there are only two words \(x_1, x_2\). At this point, we have:
\(\bar{L} = p(x_1) L(x_1) + p(x_2) L(x_2)\)
Equivalently:
\(\bar{L} = p(x_1) L(x_1) + (1 - p(x_1)) L(x_2)\)
Subject to:
- \(p(x_1) \in (0, 1)\) is a constant
- \(L(x_i) > 0, i \in \{1, 2\}\) are independent variables
- \(2^{- L(x_1)} + 2^{- L(x_2)} \le 1\)
Define \(a_1 = 2^{- L(x_1)}, a_2 = 2^{- L(x_2)}\). Now we have:
\(\bar{L} = - p(x_1) \log_2{a_1} - (1 - p(x_1)) \log_2{a_2}\)
Subject to:
- \(p(x_1) \in (0, 1)\) is a constant
- \(0 < a_i <1, i \in \{1, 2\}\) are independent variables
- \(a_1 + a_2 \le 1\)
At this point, \(\bar{L}\) can be regarded as a binary function whose independent variables are \(a_1, a_2\), and the value ranges of the independent variables \(a_1, a_2\) are as follows:
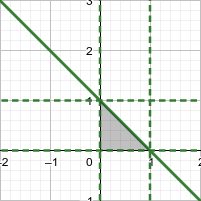
We want to find the minimum value of \(\bar{L}(a_1, a_2)\) within this range of values.
The gradient of \(\bar{L}(a_1, a_2)\) is as follows:
\(\nabla\bar{L}(a_1, a_2) = {(-p(x_1) \log{2} \frac{1}{a_1}, -(1 - p(x_1)) \log{2} \frac{1}{a_2})}^T\)
Within the value range of the independent variables \(a_1, a_2\), \(\nabla\bar{L}(a_1, a_2)\) is always less than 0, which means that with the growth of \(a_1, a_2\), \(\bar{L}(a_1, a_2)\) decreases. Therefore, the maximum value of \(\bar{L}(a_1, a_2)\) must occur when \((a_1, a_2)\) is on the boundary line \(a_1 + a_2 = 1\).
Substituting the boundary line \(a_1 + a_2 = 1\) into \(\bar{L}(a_1, a_2)\), you can get a unary function:
\(\bar{L}(a_1) = - p(x_1) \log_2{a_1} - (1 - p(x_1)) \log_2{(1 - a_1)}\)
The constraints include:
- \(p(x_1) \in (0, 1)\), constant
- \(0 < a_1 < 1\)
The derivative of \(\bar{L}(a_1)\) is as follows:
\(\frac{d \bar{L}(a_1)}{d a_1} = \frac{\log{2} (a_1 - p(x_1))}{a_1 (1 - a_1)}\)
The constraints include:
- \(p(x_1) \in (0, 1)\) is a constant
- \(0 < a_1 < 1\)
When \(0 < a_1 < p(x_1)\), \(\frac{d \bar{L}(a_1)}{d a_1} < 0\), \(\bar{L}(a_1)\) monotonically decreases, and when \(p(x_1) < a_1 < 1\), \(\frac{d \bar{L}(a_1)}{d a_1} > 0\), \(\bar{L}(a_1)\) monotonically increases. Therefore, when \(a_1 = p(x_1)\), \(\bar{L}(a_1)\) obtains the minimum value.
As \(a_1 = 2^{- L(x_1)}, a_2 = 2^{- L(x_2)}\), this means that, for:
\(\bar{L} = p(x_1) L(x_1) + (1 - p(x_1)) L(x_2)\)
Subject to:
- \(p(x_1) \in (0, 1)\) is a constant
- \(L(x_i) > 0, i \in \{1, 2\}\) are independent variables
- \(2^{- L(x_1)} + 2^{- L(x_2)} \le 1\)
\(\bar{L}\)'s minima occurs when \(L(x_1) = -\log_2{p(x_1)}, L(x_2) = -\log_2{p(x_2)}\), and the minima is \(- p(x_1) \log_2{p(x_1)} - p(x_2) \log_2{p(x_2)}\).
Going back to the multivariate optimization problem:
\(\bar{L} = p(x_1) L(x_1) + \dots + p(x_n) L(x_n)\)
Subject to:
- \(p(x_i) \in (0, 1), i \in \{1, 2, \dots, n\}\) are constants
- \(p(x_1) + p(x_2) + \dots + p(x_n) = 1\)
- \(L(x_i) > 0, i \in \{1, 2, \dots, n\}\) are independent variables
- \(2^{- L(x_1)} + 2^{- L(x_2)} + \dots + 2^{- L(x_n)} \le 1\)
\(\bar{L}\)'s minima occurs when \(L(x_i) = -\log_2{p(x_i)}, i \in \{1, 2, \dots, n\}\), and the minima is \(- p(x_1) \log_2{p(x_1)} - \dots - p(x_n) \log_2{p(x_n)}\).
Definition of Information Entropy
If a language "language" \(X\) has \(n\) "words", \(x_1, x_2, \dots, x_n\), the probability of their occurrence is \(p(x_1), p(x_2), \dots, p(x_n)\), then all "words" under a certain optimal encoding, the previously calculated minimum weighted average encoding length, \(- p(x_1) \log_2{p(x_1)} - \dots - p (x_n) \log_2{p(x_n)}\), is called the information entropy of the "language", denoted as \(H(X)\).
The reason why it is called "information entropy" is mainly due to the following reasons:
- From von Neumann's naming suggestion for Shannon: My greatest concern was what to call it. I thought of calling it 'information,' but the word was overly used, so I decided to call it 'uncertainty.' When I discussed it with John von Neumann, he had a better idea. Von Neumann told me, 'You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, no one really knows what entropy really is, so in a debate you will always have the advantage.
- In a sense, it does reflect the frequency distribution of the "words" of "language" \(X\), just as entropy in thermodynamics reflects the distribution of microscopic particles. The lower \(H(X)\) is, the more the case that only a few words are used frequently in \(X\); the higher \(H(X)\) is, the more the case that all words in \(X\) are used frequency.
Links to Explanations of Related Concepts
How These Concept are Applied in Practice
https://colah.github.io/posts/2015-09-Visual-Information/#conclusion
References
- https://colah.github.io/posts/2015-09-Visual-Information/
- https://mbernste.github.io/posts/sourcecoding/
- https://en.wikipedia.org/wiki/Kraft–McMillan_inequality
- https://mathoverflow.net/questions/403036/john-von-neumanns-remark-on-entropy